Calcul d’un prêt et d’un échéancier avec Excel
Vous souhaitez faire le calcul d’un prêt dans Excel et mettre en place un échéancier en fonction des éléments indiqués par vous-même ou un utilisateur ?
Dans cet article, vous trouverez toutes les informations pour réaliser ces deux calculs (calculer un prêt et un échéancier). Vous trouverez également un tableau avec toutes les fonctions nécessaires qu’il vous suffira de télécharger pour pouvoir appliquer. Un prêt bancaire est toujours en enjeu important, pouvoir le comprendre et le calculer est essentiel avant de se lancer.

On se pose souvent plusieurs questions lorsqu’on signe un prêt. Dans cet article, vous découvrirez comment répondre aux trois principales questions que l’on peut se demander. La première, c’est de rechercher la mensualité à payer (combien devrais-je payer par mois ?), la seconde c’est de rechercher le taux d’intérêt (quel sera le taux d’intérêt du prêt ?) et la troisième c’est la durée du prêt (combien de mensualité devrais-je rembourser ?).
Voici une solution simple (en vidéo) pour réaliser le calcul d’un prêt avec échéancier dans Excel en 30 secondes. Sinon, vous trouverez les formules et les explications dans la suite de cet article pour construire vous même votre échéancier ou récupérer un fichier exemple.
1 – Calcul de prêt pour la mensualité
2 – Calcul de prêt pour le taux d’intérêt
3 – Calcul de prêt pour la durée
4 – Décomposer un prêt
5 – Créer un échéancier du prêt
Vous pouvez télécharger le fichier Excel ci-dessous pour tester les fonctions. Celui-ci contient trois feuilles pour présenter les différents modes de calcul. Les différents calculs présents dans ces dernières sont expliqués dans l’article ci-dessous.
Ci-dessous, le fichier à télécharger contenant les formules utilisées dans cet article :
TELECHARGER LE FICHIER AVEC LES FORMULES
Le résultat final d’un calcul de prêt avec échéancier sera le suivant :
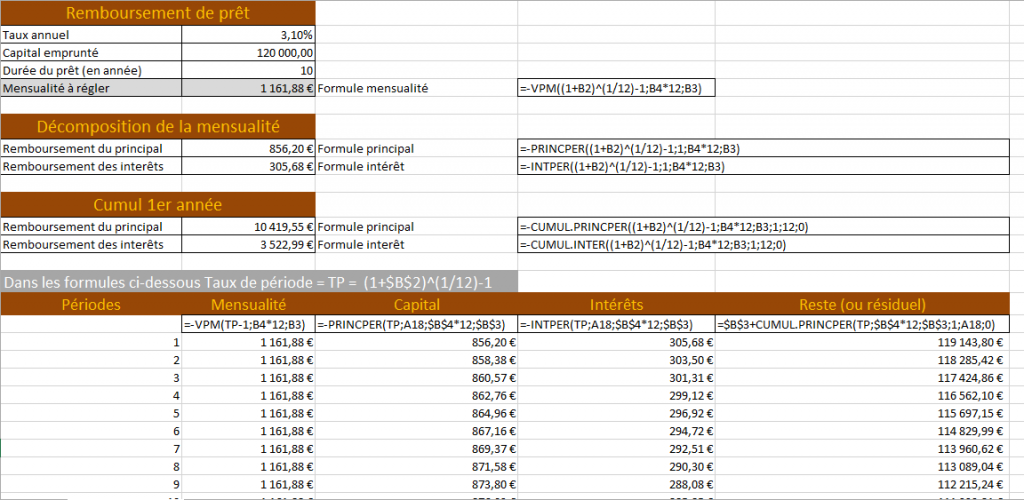
1 – Calcul de prêt pour la mensualité
Dans un premier temps, nous allons voir comment mettre en place le calcul d’une mensualité pour mon prêt. Autrement dit, en fonction du taux annuel, du capital et de la durée de celui-ci je devrais retrouver le montant à rembourser mensuellement.

La formule utilisée sera donc VPM, comme le montre la capture ci-dessus, celle-ci s’écrit de la manière suivante :
=-VPM(taux;durée;capital;[résiduelle];[terme])
Le signe moins devant VPM est nécessaire sinon la formule retourne un nombre négatif. Les trois premiers arguments sont le taux de l’emprunt, la durée de l’emprunt (nombre de périodes) et le capital emprunté. Les deux derniers arguments sont facultatifs, la valeur résiduelle est par défaut à 0 et terme, qui permet de gérer le fait que l’échéance est payée à terme à échoir (pour 1) ou à terme échu (pour 0), est lui aussi facultatif.
La formule Excel utilisée pour calculer la mensualité du prêt est donc :
=-VPM((1+B2)^(1/12)-1;B4*12;B3) équivaut à =-VPM((1+3,10%)^(1/12)-1;10*12;120000)
Explication : Pour le taux j’utilise le taux de période, qui est le taux mensuel, si vous ne savez pas de quoi il s’agit je vous invite à consulter cet article, ensuite je calcul le nombre de périodes (en mois, ici 120 car 10 ans multiplié par 12 mois) et enfin j’indique le capital emprunté. Ma mensualité sera donc de 1 161,88 euros sur 10 ans.
2 – Calcul de prêt pour le taux d’intérêt
Nous venons de voir comment mettre en place le calcul d’une mensualité pour mon prêt. Mais je pourrais très bien savoir combien je souhaite emprunté, la mensualité maximum que je puisse payer, le nombre d’années sur lesquelles je souhaite rembourser, dès lors, j’aimerais connaître le taux d’intérêt annuel que je devrais obtenir de mon banquier pour atteindre mes objectifs. La formule que nous allons voir permet de déterminer le taux annuel à obtenir en fonction des critères indiqués précédemment.

Comme le montre la capture ci-dessus, je vais dans un premier temps calculer le taux de période (le taux mensuel dans notre cas), puis dans un second le taux annuel. La formule utilisée sera TAUX, comme le montre la capture ci-dessus, celle-ci s’écrit de la manière suivante :
=TAUX(durée;mensualité;capital;[résiduelle];[terme];[estimation])
Les trois premiers arguments sont la durée de l’emprunt (nombre de périodes), la mensualité à rembourser et le capital emprunté. Les trois derniers arguments sont facultatifs, la valeur résiduelle est par défaut à 0, l’argument terme, qui permet de gérer le fait que l’échéance est payée à terme à échoir (pour 1) ou à terme échu (pour 0), est lui aussi facultatif, enfin l’argument estimation est facultatif, mais permet de donner une estimation initiale du taux.
La formule Excel utilisée pour calculer le taux du prêt est donc :
=TAUX(12*B4;-B2;B3) qui équivaut dans notre cas à =TAUX(12*13;-960;120000)
Remarque : la donnée correspondante à la mensualité doit être donnée de manière négative. C’est pourquoi un signe moins est devant dans la formule. Notre taux de période est de 0,294%
Je vais utiliser la formule =(1+B5)^12-1 soit =(1+0,294%)^12-1 pour obtenir le taux annuel de notre prêt qui sera 3,58%. Autrement dit, pour emprunter 120 000 euros sur 13 ans et afin de rembourser mensuellement 960 euros je devrais obtenir un prêt à un taux annuel de 3,58 % au maximum, si je négocie un taux en dessous c’est du bénéfice ;).
3 – Calcul de prêt pour la durée
Nous allons maintenant voir comment obtenir la durée d’un prêt lorsque l’on connaît le taux annuel, le capital emprunté et la mensualité que l’on souhaite rembourser. Autrement dit, combien de temps vais-je mettre à rembourser 120 000 euros à un taux de 3,10 % avec 1 100 de mensualité ? La formule va répondre à cette question.

La formule utilisée sera donc NPM, comme le montre la capture ci-dessus, celle-ci s’écrit de la manière suivante :
=NPM(taux;mensualité;capital;[résiduelle];[terme])
Les trois premiers arguments sont le taux annuel de l’emprunt, la mensualité à rembourser et le capital emprunté. Les deux derniers arguments sont facultatifs, la valeur résiduelle est par défaut à 0, l’argument terme, qui permet de gérer le fait que l’échéance est payée à terme à échoir (pour 1) ou à terme échu (pour 0), est lui aussi facultatif.
=NPM((1+B2)^(1/12)-1;-B4;B3) qui donne dans notre cas =NPM((1+3,10%)^(1/12)-1;-1100;120000)
Remarque : la donnée correspondante à la mensualité doit être donnée de manière négative. C’est pourquoi un signe moins est devant dans la formule. Notre durée de remboursement est de 127,97 périodes (donc en mois dans notre cas).
Je vais utiliser la formule =B5/12 soit =127,97/12 pour obtenir le nombre d’années afin d’achever le remboursement du prêt. Autrement dit, pour emprunter 120 000 euros à un taux annuel de 3,10% et afin de rembourser mensuellement 1 100 euros je devrais rembourser des échéances durant 128 mois soit 10 et 8 mois.
4 – Décomposer un prêt
Un remboursement de prêt est constitué, de deux choses, le capital et les intérêts (vous vous doutiez qu’on ne vous prêtait pas gratuitement 😉 ). Les intérêts sont calculés pour chaque période, par exemple pour des remboursements mensuels sur 10 ans, cela nous donnera 120 périodes.

La capture ci-dessus montre la décomposition d’une mensualité (une période parmi les 120) de notre prêt, pour cela, il suffit d’utiliser les formules PRINCPER et INTPER. Les arguments des deux formules sont les mêmes et se décomposent de la manière suivante :
=-PRINCPER(taux;num_période;durée;capital;[résiduelle];[terme]) =-INTPER(taux;num_période;durée;capital;[résiduelle];[terme])
Les arguments sont les mêmes que pour la formule VPM vu dans la première partie, sauf pour num_période qui est rajouté et qui permet d’indiquer la période à décomposer et ainsi connaître le capital ou les intérêts pour celle-ci. Prenons un exemple :
=-PRINCPER((1+B2)^(1/12)-1;1;B4*12;B3) qui donne =-PRINCPER((1+3,10%)^(1/12)-1;1;10*12;120000) =-INTPER((1+B2)^(1/12)-1;1;B4*12;B3) qui donne =-INTPER((1+3,10%)^(1/12)-1;1;10*12;120000)
Le résultat est celui affiché dans la capture « Décomposition de la mensualité » au dessus, la période analysée est « 1 » donc la première période, autrement dit le premier mois. Pour celui-ci, je paierais1 161,88 Euros (comme vu avec le calcul de mensualité), décomposé en 856,2o Euros de capital et 305,68 Euros d’intérêts.

Maintenant il est également possible de calculer le remboursement du capital et le remboursement de l’intérêt pour plusieurs périodes. Par exemple, les 12 premiers mois, ou les 17 premiers mois ou du 27ème mois au 42ème… Pour cela, il faut utiliser les formules
=-CUMUL.PRINCPER(taux;durée;capital;début_période;fin_période;terme) =-CUMUL.INTER(taux;durée;capital;début_période;fin_période;terme)
On retrouve les arguments taux, durée, capital et terme (qui sont obligatoires) que nous avons déjà vus en première partie avec la formule VPM. Ici, on constate l’apparition des arguments début_période et fin_période, le premier indique donc le début de la période à analyser et le deuxième argument la fin. Prenons un exemple :
=-CUMUL.PRINCPER((1+B2)^(1/12)-1;B4*12;B3;1;12;0) qui donne =-CUMUL.PRINCPER((1+3,10%)^(1/12)-1;10*12;120000;1;12;0)
=-CUMUL.INTER((1+B2)^(1/12)-1;B4*12;B3;1;12;0) qui donne =-CUMUL.INTER((1+3,10%)^(1/12)-1;10*12;120000;1;12;0)
Le résultat est celui affiché dans la capture « Cumul 1er année » au-dessus, la plage de périodes analysée va donc de 1 à 12, de la première période (premier mois) à la douzième (12ème mois), autrement dit sur une année. Sur un an je paierais donc 10 419,55 Euros de capital et 3 522,99 Euros d’intérêts.
5 – Créer un échéancier du prêt
Les formules vues auparavant vont me permettre de créer l’échéancier de mon prêt, afin de savoir période par période (donc mois par mois), combien je paierai en mensualité, en capital, en intérêts et combien me reste-t-il à payer.
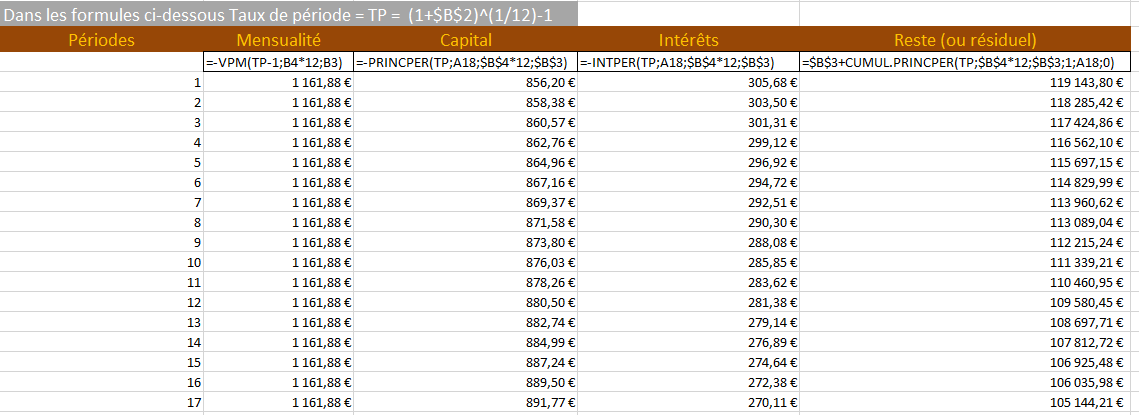
Pour cela nous allons utiliser les différentes formules vu précédemment et les faire glisser en fonction du nombre de périodes.
Dans la première colonne période, il suffit de rentrer 1 comme première période, puis de faire glisser de manière incrémentale ma cellule vers le bas, dans mon cas, j’ai besoin de 120 périodes, puisque 10 ans de remboursement de prêt multiplié par 12 mois = 120.
Dans la seconde colonne, il s’agit de la mensualité que je devrais rembourser chaque mois, celle-ci est constante sur l’ensemble du prêt. Pour la calculer, j’insère la formule suivante dans la cellule de ma première période :
=-VPM(TP-1;B4*12;B3) qui donne =-VPM((1+3,10%)^(1/12)-1;10*12;120000)
Puis dans la seconde cellule, je n’utilise pas la formule, mais simplement le numéro de la cellule contenant la formule et donc le résultat, cela me permettra de le reproduire, puis je fais glisser vers le bas.
Dans la troisième colonne, il s’agit du capital qui sera remboursé par mensualité. Par exemple, pour la 40ème période (donc 40ème mois), je rembourserais 945,51 € en capital sur ma mensualité de 1 161,88 €. Pour calculer le capital remboursé j’utilise la formule suivante :
=-PRINCPER(TP;A18;$B$4*12;$B$3) qui équivaut à =-PRINCPER((1+3,10%)^(1/12);1;10*12;120000)
Le signe $ permet de faire glisser la formule dans le champ en dessous sans décaler la cellule sinon, en faisant glisser la formule dans les autres cellules la sélection aurait été sur B5 puis B6… Le signe $ nous permet de bloquer la cellule en quelque sorte, ainsi notre cellule contenant le taux annuel sera toujours sélectionnée ainsi que la durée et le capital emprunté. TP correspond au taux de période, c’est simplement par gain de place qu’il est écrit sous cette forme.
La variable qui sera modifiée lors de la recopie de la cellule vers le bas sera donc A18, qui passera à A19 puis A20…. ce qui modifiera le numéro de période pour nous donner la période correspondante.
Dans la quatrième colonne, il s’agit cette fois des intérêts, je viens de calculer le capital remboursé sur notre mensualité, maintenant je vais savoir pour chaque période combien je paierai d’intérêt. J’utilise la formule :
=-INTPER(TP;A18;$B$4*12;$B$3) qui donne =-INTPER((1+3,10%)^(1/12);1;10*12;120000)
Le signe $ à la même vocation que pour la troisième colonne.
La variable qui sera modifiée lors de la recopie des cellules sera également A18 qui correspond au numéro de période.
Dans la cinquième colonne, je vais calculer le reste (résiduel), autrement dit, combien restera-t-il à payer après la mensualité en question. Par exemple, après la mensualité correspond à la 40ème période il me restera à payer 83 994,69 euros sur les 120 000 euros. La formule sera la suivante :
=$B$3+CUMUL.PRINCPER(TP;$B$4*12;$B$3;1;A18;0) qui donne:
=120000+CUMUL.PRINCPER((1+3,10%)^(1/12);10*12;120000;1;1;0)
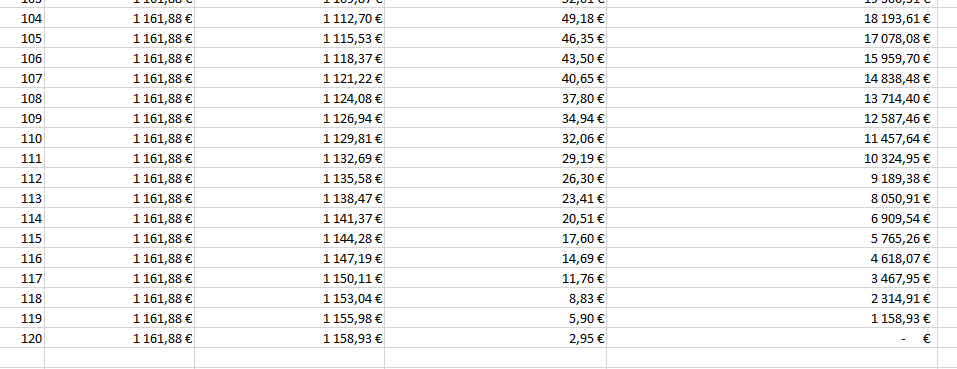
La formule utilise donc le cumul du capital selon une période avec en amont la cellule contenant le capital emprunté. Cette période commence à un et évolue lorsque je recopie la cellule vers le bas. La capture ci-dessous montre bien qu’au bout des 120 périodes (donc 120 mois qui égal 10 ans) mon prêt est remboursé.

38 Commentaires
Merci beaucoup pour les explications
De rien, avec plaisir 😉
bonjour merci beaucoup pour l’explication mais je voudrai faire une application maps sous excel et avec une base de donnée merci
Pour la base de données il faut travailler avec Access, pour une application maps, autrement-dit vous souhaitez intégrer une carte (par exemple d’une région) qui se modifie selon les données rentrées ? Si c’est bien cela je compte faire un tuto la dessus dans le courant du mois d’aout, car en ce moment je n’ai malheureusement pas le temps, donc à bientôt j’espère ;).
Merci !
Une remarque importante vis à vis de votre point n°1 : Le taux de période tel que vous le calculer { (1+B4)^(1/12)-1 } est vrai pour un taux annuel actuariel. votre formule est donc pertinente pour un prêt épargne logement où la méthode actuarielle est obligatoire pour exprimer le taux annuel.
Par contre pour les prêts bancaires, les banques expriment majoritairement leurs taux annuels avec la méthode proportionnelle. Le taux sur la période s’exprime alors simplement : B4/12.
Votre feuille Excel pourrait éventuellement être améliorée en ajoutant un menu déroulant à 2 options permettant de choisir entre l’une ou l’autre des méthodes, le choix induisant une modification de la méthode de calcul.
Encore merci pour votre article.
Merci pour la précision ;), il ne s’agit que d’une base de travail, celle-ci peut toujours être améliorée, votre remarque permettra à certain d’améliorer ce fichier à leur convenance, je vous en remercie.
Merci pour ce fichier et ce travail extra.
Merci à vous
pourrais avoir une simulation avec tva sur interets sur tableau d’amortissement sur excel
Salut à tous,
je souhaiterai entrée la date du début d’emprunt et d’automatiser le calcul de la somme des intérets jusqu’à la fin de l’année.
Exemple:
Date début: 01/11/2014
Case C23: Somme intérêts 2014 = somme (« interet de novembre » + « interet de décembre »)
Case C24: Somme intérêts 2015 de janvier à décembre
…
Avez vous une solution pour rendre la fonction dépendante de la date de début qu’on renseigne ?
merci pour cet excel
a+
Merci à vous pour le commentaire
bonjour
je souhaiterai avoir un tableau de financement avec taux de participation concessionnaire modifiable
comment faire ?
merci pour votre réponse
Bonjour,
Préférant d’abord lire les explications avant de télécharger des tableaux finis,
J’ai trouvé une grosse a une coquille dans vos exemples, dès le début pour le calcul de la mensualité du prêt.
Dans les 2 premières copies d’écran, la formule utilisée pour le calcul de la mensualité « =-VPM((1+B4)^(1/12)-1;B6*12;B5) » fait référence à des cellules vides (B6).
Dans l’état cela ne peut fonctionner. Étonnamment, personne ne la remarqué.
Merci d’avance pour vos corrections.
Bonjour,
Effectivement, petit erreur de frappe, merci pour votre remarque, j’ai fait les modifications. Je pense que personne ne l’a remarqué car la formule dans la cellule de calcul était la bonne. En tout cas merci beaucoup 😉
bonjour,
je souhaite faire calculer par excel le capital restant du à une date intermédiaire donnée avec rappel de la mensualité fixe
on rentre le montant emprunté , la durée en mois, le taux.
pouvez vous m’aider a trouver la formule
merci
Bonjour,
J’essaye de déterminer le TEG qui a été appliqué a mon prêt. Pour cela j’utilise la formule TRI. j’obtiens alors un taux périodique mensuel que je multiplie par 12 pour connaitre le taux annuel.
Or je souhaiterai savoir si Excel, lorsqu’il calcule avec la fonction TRI le taux périodique, calibre son calcul, par convention, sur une base de 30 jours ou si au contraire il considère qu’il y a 30.4166667 jours?
Cette précision est importante car si Excel fait sont calcul sur 30 jours, lorsque je multiplie ensuite par 12, comme le font d’ailleurs les banques, mon TEG n’est pas calculé sur une base de 365 jours mais seulement de 360 jours (30*12).
Merci pour votre aide.
Bonjour,
Je suis expert TEG pour le compte d’emprunteurs.
Effectivement, excel calcul sur une base de 360 jours, comme la plupart des banques. selon la méthode appelée « Lombarde »., mais il est assez simple de contourner ce point.
Toutefois… Attention. Il y a un risque en s’appuyant sur ce constat. les banques risquent de se défendre et de dire que R313-1 du code de la conso « le taux effectif global est un taux annuel, proportionnel au taux de période », soit le TEG correspond à 12 fois le taux de période en cas de remboursement mensuel. Difficile de multiplier par 12 un taux de période qui sera différent selon que le mois comporte 28 – 29 – 30 – 31 jours….
Si la loi devait être révisée, il y aurait de fortes chances qu’elle valide la pratique de l’année Lombarde… Si l’état peut venir au secours des banques… Elle ne se privera pas…
Les seuls cas où la l’année lombarde est plaidable, c’est quand le prêteur l’écrit très clairement dans ces offres. (ex la caisse d’épargne). Il n’y a plus besoin de calculs puis le prêteur écrit en toute lettre qu’il calcul ses intérêts sur la base d’une année de 360 jours
Bonjour , y a t-il une formule mathématique pour calculer le TEG?
Bonjour,
Pouvez- vous me fournir un tableau excel pour calculer mes mensualités sachant que j’emprunte 45000€ en 12 ans à un taux fixe y compris assurance de 2.1%. Merci de votre coopération.
Bonjour,
Pourriez-vous m’expliquer comment puis-je faire un tableau excel pour insérer une colonne permettant des versements exceptionnels en plus des mensualités fixe avec diminution du capital restant du.
Merci pour votre retour
Bonjour! J’aimerai savoir si vous êtes en mesure de répondre à votre propre question à l’heure actuelle? Car je me pose la même question merci!
Bonjour;
j’ai obtenu un prêt sur 30 ans avec 06 mois de différé
Pourriez vous me communiquer la formule qui s’adapte à mon cas
Merci pour votre retour
Pour info, la formule enoncée dans cet article et dans le fichier n’est pas la bonne et ne correspond pas au calcul des banques … voici la bonne :
Montant_Pret*Taux/12*(1+Taux/12)^(Nb_Mensualité*12)/(((1+Taux/12)^(Nb_Mensualité*12)-1))
s’il vous plait, comment calculer le coût du crédit bail par une fonction de la catégorie financière sur l’excel ?
je vous remercie
Bonjour,
J’aimerai faire un tableau d’amortissement mais avec une mensualité fixe et un assurance décès sur capital restant dû.
Pouvez-vous m’aider?
Merci
Bonjour,
Je cherche une formule pour connaître ma capacité d’emprunt si je connais mensualité max , taux de l’emprunt, et duréé.
Merci
Bonjour,
l’application de ces formules permet-elle de calculer l’impact d’une remise en capital, appliquée en cours de terme, sur l’amortissement total du prêt ? Si oui comment ?
Merci pour votre article
Bonjour
J aimerais savoir si je pars d un montant x amorti sur 25 ans et que le taux d’intérêt change au 5 ans dois je calculer pour 5 ans et ensuite prendre le montant restant et le mettre sur 20 ans avec le nouveau taux d intérêt ?
Merci pour ce beau travail de vulgarisation.
outre les mots barbares du monde de la finance, cela aide à se faire une petite idée de ce que l’on va leur laisser; on devrait plutôt parler de « location » que de « prêt »… car le prêt, c’est en général gratuit !
Encore des éléments de langages pour faire passer la pilule ;o)
Encore merci.
Bonjour, j’ai un souci de compréhension. Je ne sais si c’est moi qui interprète mal.
Bien. Revenons à l’exemple donné à ce lien https://www.numelion.com/taux-de-periode.html où il il y a un emprunt de 1000 euros sur 1 an à 5%. Au final, on doit donner 1050 euros à la fin d’année. Donc si je divise ce montant par 12 mois, question de vérifier. j’aurais 1050/12=87,5 euros mensuel.
Maintenant, j’applique cela à la formule ci-dessus =-VPM((1+5%)^(1/12)-1;1*12;1000) et je trouve 85,56 et si j’effectue l’opération suivante : 85,56 * 12 = 1026,72. D’où mon incompréhension.
C’est le même cas pour l’exemple ci-dessus. En tant que profane, j’emprunte 120000€ à rembourser sur 10 ans avec un taux de 3,10%.
Pour trouver le montant mensuel sans taux, je fais 120000/(10*12)=1000€ mensuel. J’applique à cela le taux qui est : 1000+(1000*3.10%)=1031. Et au final, je rembourserais 1031*120=123720€. Or si je prends le résultat ci-dessus et que j’effectue l’opération 1161,88*120=139425,6.
Je vous en prie. Éclairez ma materne. Merci pour votre bonne compréhension.
Cdt
Bjr.
Concernant le calcul de prêt sur la mensualité, supposons que la durée du prêt est par exemple sur 06 mois, quelle formule devrait-on entrer?
Est ce que celle-ci est juste?
=-VPM((1+3,10%)^(1/12)-1;6;120000)
Merci pour votre compréhension.
Cdt
Bonjour,
C’est juste pour vous remercier pour le contenu de vos publications.
Très bonne continuation
Merci beaucoup
Merci pour les explications claires.
Comment puis-je ajuster le tableau pour faire en sorte d’inclure un remboursement occasionnel de capital, par exemple à la suite de l’obtention d’un boni, diminuer le capital dû et voir l’impact sur le délai de remboursement?
Bonjour
Super article ! Je recherche pour ma part comment calculer le montant d’un prêt à partir du montant de l’échéance, de la durée et du taux d’intérêt. Pouvez-vous m’aider ?
Je suis content de vos formules que avez partager. Ça m’a donné une très bonne aperçu lors des augmentations du taux d’intérêt.