Test du khi deux (ou khi carré) dans Excel
Dans ce tutoriel nous allons voir comment réaliser un test du khi deux (ou khi carré) dans le logiciel Excel. Nous allons voir qu’il faut plusieurs phases pour obtenir le résultat.
Pour ceux qui se demandent à quoi peut bien servir le test du khi deux (ou khi carré), il s’agit d’un test d’indépendance entre deux variables. Autrement dit, celui-ci va nous permettre de déterminer si oui ou non il y a un lien entre nos variables.
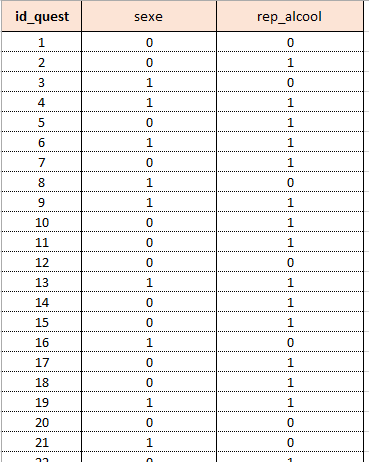 Dans notre cas, le test sera réalisé sur les résultats d’un sondage. Celui-ci comportait deux questions, la première demandait le sexe de la personne répondant au questionnaire et la seconde si cette même personne avait déjà oui ou non consommée de l’alcool sur son lieu de travail (l’abus d’alcool est dangereux pour la santé 😉 ), quand je dis alcool cela comprend bien évidemment pot de départ, repas d’affaires…
Dans notre cas, le test sera réalisé sur les résultats d’un sondage. Celui-ci comportait deux questions, la première demandait le sexe de la personne répondant au questionnaire et la seconde si cette même personne avait déjà oui ou non consommée de l’alcool sur son lieu de travail (l’abus d’alcool est dangereux pour la santé 😉 ), quand je dis alcool cela comprend bien évidemment pot de départ, repas d’affaires…
Nous avons obtenu 109 réponses au questionnaire (il est fictif je précise), les réponses sont contenues dans un formulaire.
A partir de là, nous allons essayer de déterminer si il y a un lien entre nos deux variables, autrement dit, y a t-il un lien entre le sexe de la personne interrogée et la consommation d’alcool sur le lien de travail.
Les réponses du formulaire sont représentées sous la forme 0 et 1 pour les deux questions. Pour la première question 0 correspond aux femmes et 1 aux hommes, pour la deuxième réponse 0 correspond aux personnes ayant déjà bu de l’alcool sur leur lieu de travail et 1 celles qui ne l’ont jamais fait.
Pour réaliser notre test du khi deux (ou khi carré) nous allons effectuer plusieurs étapes :
1 – Réaliser un tableau croisé dynamique
2 – Calcul des fréquences théoriques
3 – Calcul du khi deux (ou khi carré)
4 – Recherche du khi deux (ou khi carré) critique
5 – Autre calcul du khi deux (ou khi carré)
Vous pouvez consulter la vidéo ci-dessous qui résume les différentes étapes :
Voici les deux fichiers si vous souhaitez suivre les étapes, le premier est l’exercice vierge, le second la solution :
[one_half]
FICHIER POUR REALISER EXCERCICE
[/one_half][one_half_last]
[/one_half_last]
1 – Réaliser un tableau croisé dynamique
Je pense que vous savez déjà réaliser un tableau croisé dynamique sous Excel. Il va nous permettre de dépouiller rapidement les données du sondage. Notre tableau dynamique va nous donner répartition des deux variables (nos deux réponses de formulaires). Ainsi, nous serons, combien de femmes ont répondu oui ou non et combien d’hommes ont répondu oui ou non. Dans un second temps, cela nous permettra de réaliser le calcul des fréquences théoriques.
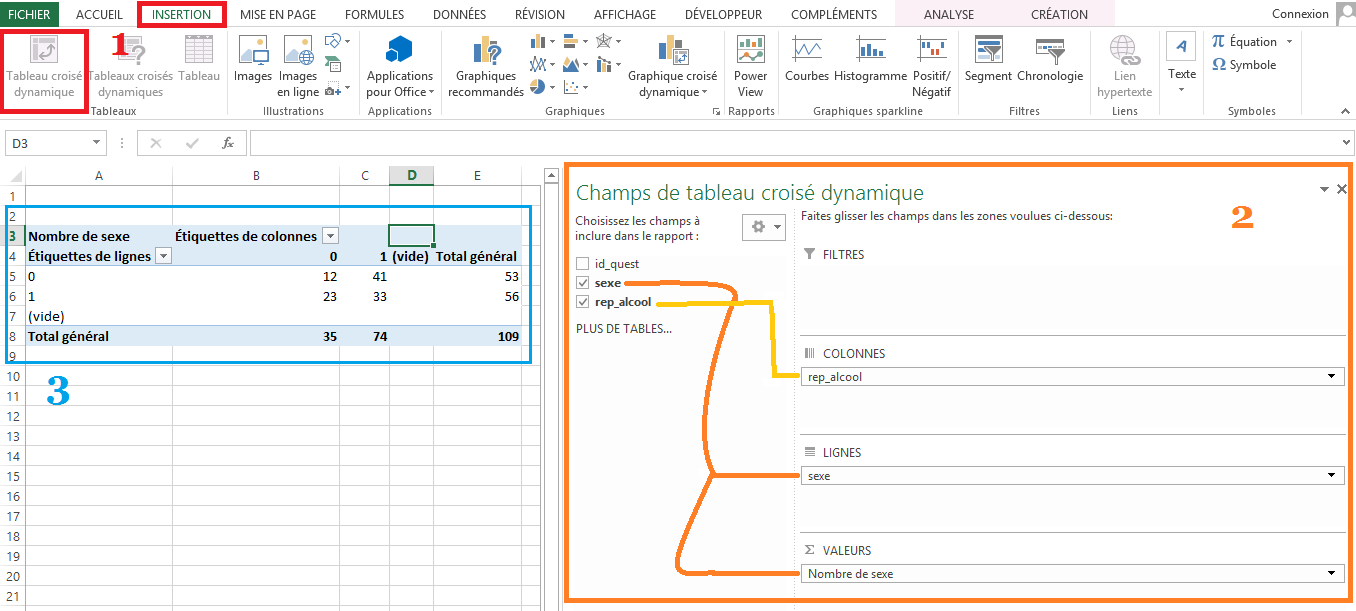
L’illustration ci-dessous présente la mise en forme du tableau croisé :
– L’étape une symbolisée par le 1 en rouge présente comment créer le tableau dynamique, dans l’onglet insertion, cliquez sur « Tableau croisé dynamique », cela devrait vous sélectionner l’ensemble des données. Si c’est le cas, validez la saisie, sinon sélectionnez l’ensemble des données du sondage et valider.
– L’étape deux (en orange sur l’illustration ci-dessous) permet de mettre en forme le tableau croisé dynamique, vous aurez une interface similaire à celle ci-dessous pour créer votre tableau, dans un premier temps, sélectionnez la variable sexe et faite la glisser dans le champ LIGNES, puis vous pouvez la sélectionner à nouveau et faite la glisser dans le champ VALEURS, vérifier que l’opération du champ VALEURS est bien sur nombre (cela nous indiquera donc le nombre de réponses par sexe). Ensuite, sélectionnez la variable rep_alcool et glissez là dans le champ COLONNES.
– Enfin, l’étape trois (en bleu sur la capture ci-dessous) nous fait apparaître le résultat de notre tableau croisé dynamique. Ainsi, on apprend, entre autres, que 56 hommes ont répondus contre 53 femmes, où par exemple que 35 personnes sur les 109 ont déjà bu sur leur lieu de travail. Notre tableau dynamique a donc dépouillé les données pour nous.
2 – Calcul des fréquences théoriques
Les fréquences théoriques correspondent aux fréquences que l’on obtiendrait si nos deux variables étaient indépendantes. Autrement dit, sans lien entre nos variables, donc entre le sexe et la consommation d’alcool, nous devrions logiquement obtenir le même pourcentage de réponses positives et négatives chez les hommes et chez les femmes.
Maintenant, nous retournons sur notre première feuille, dans celle-ci copiez / collez le tableau croisé dynamique que nous avons créé précédemment, et remplacer les 0 et 1 par les véritables variables correspondantes, autrement dit, remplacez les 0 et les 1, le résultat devrait être celui ci-dessous :
Pour calculer les fréquences théoriques nous avons besoins de connaître le pourcentage des personnes ayant répondus à oui ou à non à notre question sur l’alcool.
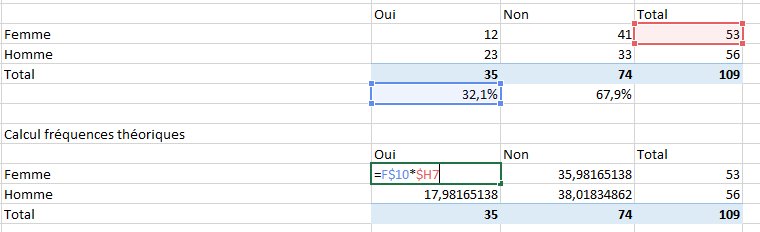
Pour cela, sélectionnez la variable « Total de oui » représentée par F9 et divisez là par le « Total de réponse » représenté par H9. La formule dans la case rouge sous le tableau (comme sur la capture ci-dessous) est donc =F9/$H9. Le signe $ permet de faire glisser la formule dans le champ à côté (pour obtenir les 67,9%) sans décaler la case H9 du calcul sinon la division aurait eu lieu en H10. Nos pourcentages sont donc 32.1 % des personnes ont dit oui quand 67.9 % ont dit non.
Passons maintenant au calcul des fréquences théoriques dont nous aurons besoins pour le calcul du khi deux (ou khi carré). Recopier le tableau ci-dessus sans les pourcentages que nous venons de calculer.
La capture ci-dessous vous montre comment obtenir les fréquences théoriques, pour la réponse oui des femmes il faut multiplier le pourcentage de notre colonne par celle de notre ligne dans notre premier tableau. Le signe $ permet de bloquer le déplacement de la ligne pourcentage et de la colonne Total, sans cela une erreur apparaitrait.
Faites glisser le calcul en bas et sur le côté pour obtenir les fréquences théoriques des oui et non selon les hommes et les femmes. Le résultat devrait être le suivant :
3 – Calcul du khi deux (ou khi carré)
Nous allons passer au calcul du khi deux (ou khi carré). La capture ci-dessous vous présente la méthode de calcul. Il faut dans un premier temps représenté une nouvelle fois le tableau croisé dynamique. Nous allons donc compléter les différentes cases.
Pour effectuer le calcul sélectionnez la case du oui pour les femmes, nous allons insérer une formule qui va calculer la portion du khi deux (ou khi carré) pour les femmes ayant déjà consommées de l’alcool sur leur lieu de travail.
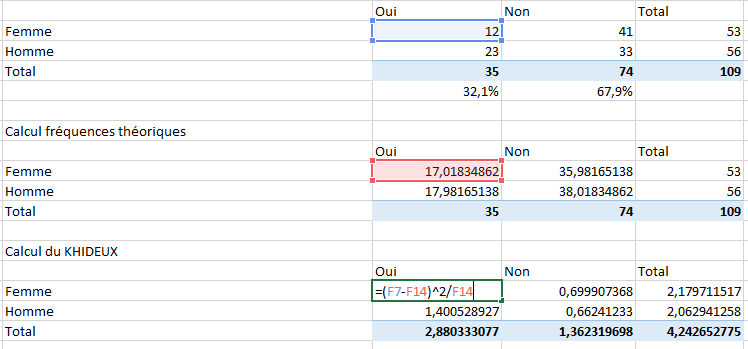
La formule est la suivante : (femmes_ayant_bu – freq_theorique_femmes_ayant_bu)² / freq_theorique_femmes_ayant_bu
En langage Excel, et pour notre configuration cela sera représenté par la formule =(F7-F14)^2/F14. Le chapeau suivi du deux permet de calculer le carré. Faites glisser la formule pour les données concernant les femmes et les hommes ayant répondu oui ou non, mais pas dans les colonnes Total. La capture ci-dessous montre le tableau du khi deux (ou khi carré) entièrement rempli, mais le calcul des colonnes total sera présenté juste après.
Pour calculer les colonnes « total », il suffit de faire pour chaque colonne du tableau la somme et de même pour chaque ligne. Exemple le total des non est donc la somme de 0,699907368 et 0,66241233. La capture si dessous vous montre les sommes à effectuer en fonction des lignes et colonnes par le biais de couleurs (c’est vraiment au cas où vous n’auriez pas compris 😉 ).
Notre khi deux (ou khi carré) apparaît dans la somme des colonnes et lignes « total », il s’agit du chiffre 4,242652775. Nous venons donc de calculer notre khi deux (ou khi carré), mais encore faut-il s’en servir.
4 – Recherche du khi deux (ou khi carré) critique
Nous allons maintenant tester l’indépendance de nos variables. Pour cela nous allons rechercher la valeur critique du khi deux (ou khi carré). Au-delà de cette valeur, nous allons rejeter l’hypothèse nulle H0. Mais vous allez me dire, c’est quoi H0 ?
Nous pouvons envisager deux résultats pour nos hypothèses, il s’agit de l’hypothèse nulle H0 et de l’hypothèse alternative H1. Notre hypothèse H0 indique qu’il n’y a pas de lien entre les variables sexe et la consommation d’alcool sur le lieu de travail. Notre hypothèse H1 indique quand ta elle qu’il y a un lien entre le sexe et le fait de consommer de l’alcool sur le lieu de travail.
Nous allons donc soit rejeter H0 soit accepter H0, autrement dit, soit valider une relation entre les variables (rejeter H0) soit ne pas conclure à une relation entre les variables (accepter H0). Si vous ne comprenez pas encore ce fonctionnement, je vais détailler le processus et la phrase de conclusion vous permettra certainement d’y voir plus clair.
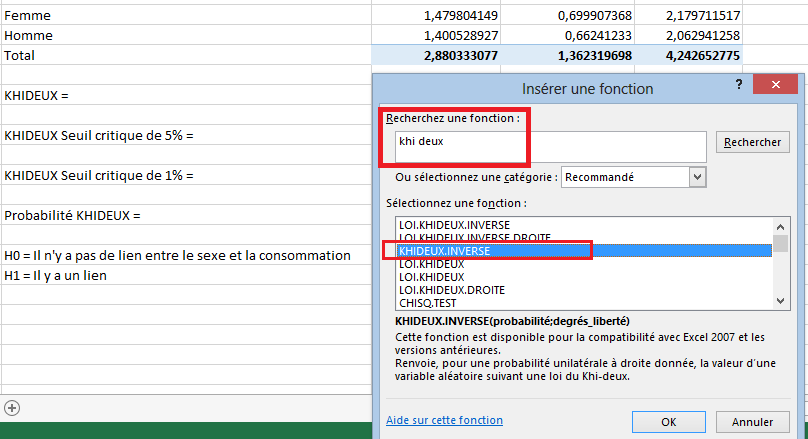
Dans un premier temps, sélectionnez une cellule dans laquelle vous souhaitez faire apparaître le résultat, puis utilisez l’icône (fx) pour sélectionner une fonction. Une fenêtre comme celle sur la capture ci-dessous devrait apparaître. Dans le champ « Recherchez une fonction » indiquez « khi deux » puis cliquer sur rechercher, cela vous affiche dans le champ en dessous les fonctions en rapport avec le mot clé khi deux. Sélectionnez la fonction KHIDEUX.INVERSE puis validez.
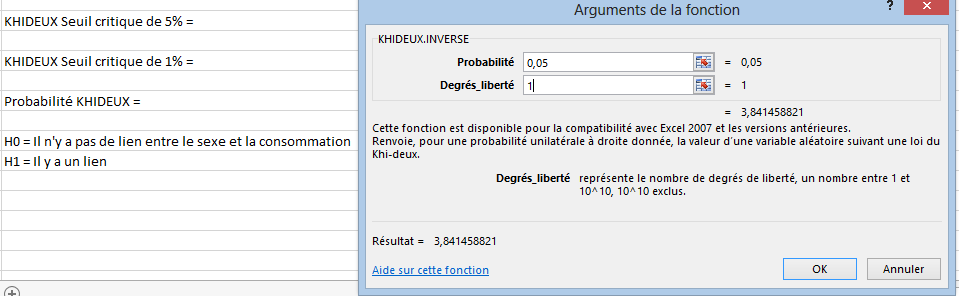
Vous arrivez sur la fenêtre permettant de renseigner les paramètres de la fonction. Vous avez deux informations à compléter, la probabilité et Degrés_liberté. La probabilité représente le seuil de signification, généralement on utilise 5% et 1%, soit 0,05 et 0,01. Il s’agit du risque d’erreur que l’on est prêt à accepter. Pour le degré de liberté vous pouvez utiliser la formule :
dl = (nombre de catégories de la 1 variable – 1) * (nombre de catégories de la 2ème variable – 1). Dans notre cas chaque variable compte deux catégories (hommes / femmes et la réponse oui / non) donc cela donne dl = (2-1) * (2-1) = 1 * 1 = 1. Notre degrés_liberté est donc 1.
La capture montre donc les informations à indiquer pour un seuil de signification de 5%.
La capture ci-dessous montre le résultat avec le paramètre probabilité à 5% (donc 0,05) et 1% (donc 0,01), le résultat est de 3,841458821 pour le paramètre à 5% et 6,634896601 pour 1%. Les conclusions que l’on peut en tirer sont les suivantes :
Avec un seuil de 5% notre résultat est de 3,84, la règle veut que si notre khi deux (4,242652775), calculé précédemment, est supérieur à 3,84 (la valeur que nous venons de calculer avec 5%) alors on rejette H0. On rejette donc le fait qu’il n’y est pas de lien entre les variables.
Pour faire une conclusion, comme H0 est rejeté, on peut en conclure avec un risque d’erreur de 5% qu’il existe un lien entre le sexe des répondants et la réponse à notre question sur la consommation d’alcool sur le lieu de travail.
Pour le seuil de 1%, je pense que vous avez compris, 6,63 étant supérieur à notre khi deux (4,24), H0 n’est pas rejeté, donc on peut conclure qu’avec un risque d’erreur de 1% , le résultat obtenu ne nous permet pas de conclure qu’il y a un lien entre le sexe et la réponse à notre question sur la consommation d’alcool sur le lieu de travail.
A la question, existe-t-il un lien entre les deux variables, à un seuil de signification de 5% oui mais à 1% non donc se sera au statisticien de juger en sélectionnant un risque d’erreur qui lui semble acceptable.
5 – Autre calcul du khi deux (ou khi carré)
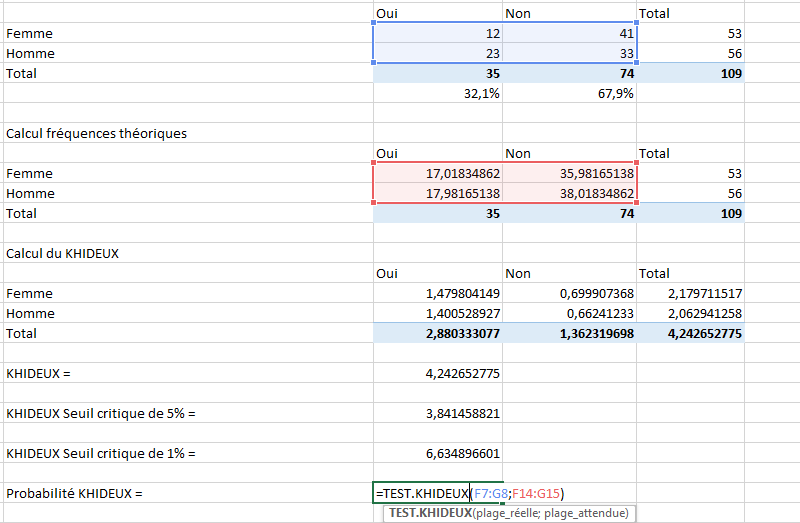
Il existe une autre façon, beaucoup plus rapide pour effectuer notre test. Il faut utiliser la fonction Excel TEST.KHIDEUX. Elle va nous permettre de calculer l’air à droite de notre khi deux calculé précédemment. On pourra ainsi déterminer le pourcentage au dessus de celui-ci. Vous pouvez soit utiliser l’icône (fx) comme dans l’exemple précédent, soit utiliser directement la formule dans une cellule comme dans la démonstration ci-dessous :
Sur la capture ci-dessus, on constate qu’il faut utiliser la fonction TEST.KHIDEUX et indiquer en paramètre la plage des valeurs de notre premier tableau qui correspond au tableau des fréquences observées, insérer un point virgule puis la plage des valeurs du tableau des fréquences théorique.
La formule est : =TEST.KHIDEUX(valeurs_tableau_frequence_observees;valeurs_tableau_frequences_theoriques)
Le résultat est donc de 0,039420526353728 qu’il suffit de convertir en pourcentage pour obtenir 3,942%.
Le résultat signifie donc qu’il y a 3,942% au dessus de notre khi deux (ou khi carré). Le défaut de cette formule est que nous ne connaissons pas la valeur du khi deux (ou khi carré), il faut utiliser la méthode précédente pour le connaître, mais elle nous permet de comprendre pourquoi H0 à été rejeté avec le seuil de signification à 5% et pourquoi il ne l’a pas été avec le seuil de signification à 1% puisque 3,942% se trouve entre les deux.







20 Commentaires
Merci beaucoup, c’est très ludique et bien expliqué !
Merci 😉
Mon sauveur pour le mémoire !!!
Avec plaisir 😉
Merci beaucoup !! C’est très clair et bien expliqué !
Merci à vous
Bonsoir,
Un très grand merci pour ce tutoriel très clair, précis et qui m’a bien aidée pour mon mémoire ! Je ne sais pas si ça vous semble envisageable mais je le tente : pensez-vous que nous puissions nous contacter afin que vous me confirmiez que je ne me suis pas trompée dans l’application et l’interprétation du khi-deux ? Car je ne connais personne capable de vérifier que je n’ai pas écrit de grosses bêtises … Quoi qu’il en soit, merci encore 🙂
Merci énormément pour vos explications, mais je ne suis pas très convaincue par le calcul des fréquences. Est ce normale que la fréquence des femmes ne buvant pas soit inférieure à la fréquence des hommes ne buvant pas alors que l’on a 41 femmes ne buvant pas contre 33 hommes.
Merci cela a beaucoup aidé mon prof a faire son « cours »
😉
Limpide ! Merci pour ce travail didacticiel.
Merci à vous pour votre soutien
Merci pour ce sympathique tuto’.
Pour compléter ce que vous dites sur la 2e méthode (avec la fonction Excel) : « Le défaut de cette formule est que nous ne connaissons pas la valeur du khi deux (ou khi carré) »
–> Oui, mais des tables standard de Khi2 existent ! Avec un grand nombre de degrés de liberté et de % d’erreur. Il est dont facile d’utiliser la fonction Excel puis comparer aux valeurs de la table.
Absolument parfait. Je suis en stage en finance et vous m’avez sauvée la vie !!
De rien, c’est avec plaisir. Bon courage pour la fin de votre stage 😉
Bonjour, quand le khi carré est bien supérieur (de l’ordre de la dizaine ou centaine) au khi carré calculé sur Excel, cela signifie-t-il que la relation n’existe pas ?
Merci pour votre vidéo explicative. Elle est d’une grande aide !
Bonjour,
Merci grandement pour cette page et cette explication qui m’a permis de me comporter face à mes données. Merci aussi pour votre vidéo explicative. Je ne fais que vous jeter des fleurs!! Loving
Merci beaucoup pour votre tuto très clair, nous allons réussir not études grâce à vous, bonne soirée !
nos*
Merci beaucoup,pour cette explication très clair et simple.